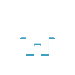一亩二百步十一分步之七。

    ○大广田

    〔淳风等按：大广田知，初术直有全步而无余分；次术空有余分而无全步；

    此术先见全步，复有余分，可以广兼三术，故曰大广。〕

    术曰：分母各乘其全，分子从之，

    〔分母各乘其全，分子从之者，通全步内分子。如此则母、子皆为实矣。〕

    相乘为实。分母相乘为法。

    〔犹乘分也。〕

    实如法而一。

    〔今为术广从俱有分，当各自通其分。命母入者，还须出之，故令分母相乘

    为法而连除之。〕

    今有圭田广十二步，正从二十一步，问为田几何？答曰：一百二十六步。

    又有圭田广五步二分步之一，从八步三分步之二，问为田几何？答曰：二十

    三步六分步之五。

    术曰：半广以乘正从。

    〔半广知，以盈补虚为直田也。亦可半正从以乘广。按：半广乘从，以取中

    平之数，故广从相乘为积步。亩法除之，即得也。〕

    今有邪田，一头广三十步，一头广四十二步，正从六十四步。问为田几何？

    答曰：九亩一百四十四步。

    又有邪田，正广六十五步，一畔从一百步，一畔从七十二步。问为田几何？

    答曰：二十三亩七十步。

    术曰：并两斜而半之，以乘正从若广。又可半正从若广，以乘并。亩法而一。

    〔并而半之者，以盈补虚也。〕

    今有箕田，舌广二十步，踵广五步，正从三十步，问为田几何？答曰：一亩

    一百三十五步。

    又有箕田，舌广一百一十七步，踵广五十步，正从一百三十五步，问为田几

    何？答曰：四十六亩二百三十二步半。

    术曰：并踵、舌而半之，以乘正从。亩法而一。

    〔中分箕田则为两邪田，故其术相似。又可并踵、舌，半正从，以乘之。〕

    今有圆田，周三十步，径十步。

    〔淳风等按：术意以周三径一为率，周三十步，合径十步。今依密率，合径

    九步十一分步之六。〕

    问为田几何？答曰：七十五步。

    〔此于徽术，当为田七十一步一百五十七分步之一百三。

    淳风等按：依密率，为田七十一步二十三分步之一十三。〕

    又有圆田，周一百八十一步，径六十步三分步之一。

    〔淳风等按：周三径一，周一百八十一步，径六十步三分步之一。依密率，

    径五十七步二十二分步之一十三。〕

    问为田几何？答曰：十一亩九十步十二分步之一。

    〔此于徽术，当为田十亩二百八步三百一十四分步之一百十三。

    淳风等按：依密率，当为田十亩二百五步八十八分步之八十七。〕

    术曰：半周半径相乘得积步。

    〔按：半周为从，半径为广，故广从相乘为积步也。假令圆径二尺，圆中容

    六觚之一面，与圆径之半，其数均等。合径率一而外周率三也。

    又按：为图，以六觚之一面乘一弧半径，三之，得十二觚之幂。若又割之，

    次以十二觚之一面乘一弧之半径，六之，则得二十四觚之幂。割之弥细，所失弥

    少。割之又割，以至于不可割，则与圆周合体而无所失矣。觚面之外，又有余径。

    以面乘余径，则幂出觚表。若夫觚之细者，与圆合体，则表无余径。表无余径，

    则幂不外出矣。以一面乘半径，觚而裁之，

『加入书签，方便阅读』